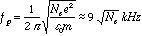 (1)
(1)
The alternative to in-situ measurements is remote sensing. Remote sensing of ionospheric and magnetospheric processes continues to mature with recent advances in technology. Until recently, passive sensing has been largely limited to auroral regions and solar physics. Active radio sounding provides a way to extend remote sensing to the rest of the magnetosphere [1], while trivially resolving the ambiguity between spatial variations and temporal variations. Active radio methods directly provide differential rather than column integrated measurements, complementing the optical, UV, and neutral particle imagers now available. Radio sounding also provides an opportunity to simultaneously measure widely separated regions of the magnetosphere. As we describe below, an active radio plasma sounder presents a unique opportunity to simultaneously study small and large scale magnetospheric plasmas.
Complementing the long heritage of ground based sounders, a number of space based "topside" ionospheric sounders have been flown. Beginning with the Alouette/ISIS programs in 1962 [3], topside sounders have included Alouette 1/2, ISIS 1/2, ISS-b, EXOS-C/D, Intercosmos 19, and Cosmos 1809. During its first 3 years on orbit, Alouette 1 alone provided 1100 ionograms each day. Although the intent of the Alouette/ISIS program was to study the upper ionosphere, ISIS also demonstrated the ability to remotely sound the magnetospheric cusp [4]. A new generation of space borne sounders could use the technology of modern ground based sounders to provide a new way to observe multiscale magnetospheric plasmas.
In addition to avoiding spatial/temporal aliasing, radio sounding offers several other advantages. Most importantly, a sounder can sample points not at the spacecraft location, including points not on the spacecraft trajectory. This allows sounders to sample more regions than comparable in-situ measurements, and reduces the coupling between the orbit period and the observable time scales. Since radio sounders can perform simultaneous measurements of remotely separated regions, sounding may greatly improve our understanding of the coupling between the many regions and processes in the solar/terrestrial system.
One of the most significant advantages of active radio sounding of the magnetosphere is the large range of scales that can be observed by a single instrument. For illustrative purposes, we will consider a 10W magnetospheric sounder (less than 10% of the transmitted power of Alouette-1) with 400m dipole antennas. Using sounding frequencies from 3 kHz to 3 MHz allows detection of reflections from a range of plasma densities greater than seen in the magnetosphere. Calvert et al.═s analysis [5] (hereafter referred to as Calvert) showed that a digital radio sounder with these characteristics could resolve density structures as small as 500 km at distances of up to 4 RE from the sounder. Under appropriate conditions, a sounder can measure the positions, density profiles, velocity profiles, and field strength profiles of both flanks of the magnetopause/boundary layer simultaneously (across a total of 30 RE). It can resolve plasma structures on scales ranging from 0.08 RE to 30 RE, including line of sight density, field strength, and velocity profiles, in minutes. This is a tremendous improvement over in-situ measurements, which provide only local density and field measurements. These one-dimensional profiles can also be combined to build detailed planar sections of magnetospheric regions on time scales of 1 orbit.
The crucial distinction between these two modes for magnetospheric sounding is that the O mode cutoff is determined solely by the plasma density, while the X mode cutoff is also a function of the total magnetic field strength. The cutoff for the O mode is the local plasma frequency fp,
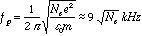 (1)
(1)
when the electron density Ne is expressed in cm-3; eo is the permittivity of free space, e is the electron charge and m is the electron mass. For the X mode, the cutoff fx is
 (2)
(2)
where the gyrofrequency is fg = (1/2p)eB/m ü 28 B (Hz) when B, the magnetic field strength, is expressed in nT. These two modes propagate freely with group velocity vg >> vph >> c when the wave frequencies are well beyond the mode cutoffs; thus they are also called the free-space modes.
For a sounder in the magnetospheric cavity, where the density and field strengths are relatively low, the sounding frequencies are well above the local plasma frequency. Both wave modes travel at their group velocities, which are nearly c in this region. The O mode group velocity is:
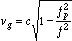 (3)
(3)
The X mode group velocity includes the effect of the magnetic field, but is approximately given by equation (3) throughout the sounding region.
O mode cutoff, hence reflection, occurs at regions of increased plasma density such as the plasmasphere or boundary layers. At each point where the plasma frequency equals the sounding frequency, the wave will be reflected. If the density gradient points away from the sounder, the wave will be reflected in the direction of the sounder and detected. For the X mode, an additional term depending on the magnitude of the magnetic field is added, but the process is otherwise identical. Thus, at each frequency several O (and X) mode returns will be detected at the spacecraft. For each return, the sounder measures the delay time (distance), Doppler shift (line of sight velocity), and the direction from which the return is received. The sounder then increments the transmitted frequency, and detects more distant, higher density layers. Since the propagation speed is comparable to c except near the reflecting gradient, the sounder can very rapidly build up detailed profiles of even very remote regions. For the X mode wave the process is very similar, and the returns can be compared to the O mode data to distinguish magnetic field and plasma density variations [10].
Given the ability to distinguish between the plasma density and field strength of remote plasmas, the question remains as to which magnetospheric structures and phenomena could be detected with a radio sounder. Most magnetospheric regions and structures have X and O mode cutoffs between 3 kHz and 3 MHz:
| Region | Density (cm-3) |
|B| (nT) |
O Mode cutoff (kHz) |
O Mode cutoff (kHz) |
| inner plasmasphere | 104 | 103 | 900 | 914 |
| plasmapause | 100 | 500 | 90.0 | 97.3 |
| outer plasmasphere | 20 | 200 | 40.3 | 43.2 |
| plasmoids | 10 | 20 | 28.5 | 28.7 |
| weak ring current | < local | dB~10 | 90.0 | 91.4 * |
| strong ring current | < local | dB~300 | 90.0 | 94.3 * |
| boundary layers | 10-20 | 40 | 34.9 | 35.4 |
| magnetpause | 20-40 | 40 | 49.3 | 49.9 |
| plasma sheet | 1 | < 50 | 9.0 | 9.7 |
| cusp | 5-10 | 0-20 | 24.7 | 24.8 |
| lobes | 0.1 | 20 | 2.9 | 3.1 |
| convective flow | 3 | 50 | 15.6 | 16.3 * |
| FTE | 20 | 10 | 40.3 | 40.4 * |
* indicates events distinguishable via secondary characteristics of the return (Doppler, etc.); the ring current is detected by means of X-mode echoes.
Table 1. Illustrative X and O mode cutoffs by region
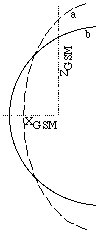
The first figure shows schematically how a sounder might be used to study plasmasphere refilling. Since it can resolve both the large scale plasmaspheric structure and the fine scales needed to measure density gradients, under appropriate conditions a sounder could directly observe plasmasphere erosion and refilling. Since the dielectric properties of the ambient plasma only support two long distance (non-trapped, non-evanescent) sounding modes, and since the sounding frequencies in these modes encompass all major magnetospheric structures, it is theoretically possible to sound most of these regions. The implementation of sounding and the geometries of the echo returns are the remaining key issues.
One of the modifying factors to the d-2 power law is focusing/defocusing by the reflecting surface. If the critical frequency surface (which is an isodensity surface for O mode waves) presents a concave surface towards the sounder, the echo return will be enhanced. This is obviously the case for sounding the magnetopause and boundary layers, where the focusing factor could increase the echo strength by a factor of ~2.8. The plasmasphere, on the other hand, will appear convex to a sounder located in the tail lobes or most magnetospheric cavities, and will return less than if this factor were neglected. If the plasmasphere were a simple 4 RE sphere, the defocusing could reduce the signal by approximately a factor of 1/2 for a sounder 1 RE beyond the plasmapause [5]. Of course the plasmasphere is not a sphere, and a sounder is likely to be much closer to the plasmasphere than to the magnetopause (see however [11,12]).
Again assuming a 10W transmitter, orthogonal 400m spin plane dipoles, and a much shorter spin axis antenna, Calvert determined that reactancetuned and impedance-matched antennas were essential. To verify the feasibility of tuning and matching 400m dipoles to existing sounder transmitter and receiver circuits at the frequencies needed, B. Reinisch and others successfully constructed and tested the proposed dipole with modified Digisonde circuitry in an end-to-end test [13]. Calvert also identified several other operational techniques and signal processing methods from ground based sounding as appropriate for magnetospheric operations. Since the waves propagate at speeds close to c, a sounder can significantly reduce noise by combining repeated measurements (digital signal integration) despite the long distances to the reflecting surfaces. Further, modern sounders use onboard processing to perform techniques such as pulse compression and spectral integration to dramatically improve signal to noise ratios. These techniques have been used in many ground-based ionosondes, providing confidence in the methods and in the resulting gains in the signal to noise ratio.
Another key feature of modern digital sounders, which could prove valuable in magnetospheric sounding, is their ability to automatically adjust their operations and transmissions. This can be used to minimize the effect of auroral kilometric radiation (AKR), which occurs at discrete frequencies [14-15]. Modern sounders can receive without transmitting, and adjust their operations to avoid noisy frequencies. This technique is used in ground based sounders to minimize the effects of man-made signals. A somewhat thornier problem is posed by continuum radiation. Escaping continuum radiation is, despite its name, also discrete [16], and can be avoided by frequency side-stepping, as for AKR. The trapped continuum, however, is too smooth in frequency to be avoided by this method. However, by its nature it tends to be trapped near the equatorial plane between the density gradients at the plasmapause and the magnetopause [17]. Thus the signal to noise ratio may be worse when operating near the equatorial plane. It is also reasonable to avoid transmitting near the equator, so that the sounder signal will not contribute to the trapped continuum.
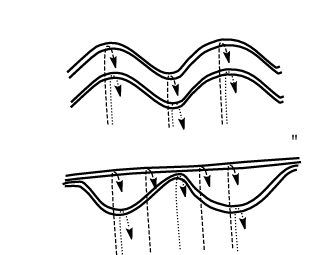
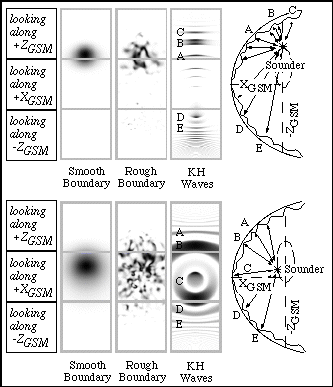
The first uses a modified optical raytracer in an optical analog of a Stern [18] magnetosphere. Since the sounding frequency is well above the ambient plasma frequency except near the reflection points, this technique should provide a realistic idea of where returns might be expected for a magnetospheric sounder. It includes simple models of the cusps, ring current, plasmasphere, magnetopause and boundary layers. The models are adjustable to simulate different solar wind conditions (Fig. 2), sounding frequencies, and sounder locations. It includes reflection, focusing, and numerical tracing of ray paths to produce 'sky maps' of echo return strengths (Fig. 3). The only effect not included in this raytracing simulation is the refraction at points other than the reflection point. As noted, this is effectively a 'high frequency' approximation. Its primary advantage is that it provides a test of the geometric optics of waves in the magnetosphere, without excessive computational requirements. It also cannot produce plasmagrams.
The more accurate of the two raytracers used to simulate magnetospheric sounding, the GSFC raytracer, was developed specifically to trace plasma waves in the magnetosphere [20]. This simulation does not currently include a ring current, or cusp models, although these may be added to future revisions of the software [23]. It does include refraction at every step in the ray path, as the dielectric properties vary. This tool been evolving since the early 1970's, and been applied to a variety of problems in terrestrial and non terrestrial magnetospheres [8-10] resulting in over 25 publications. Simulations of plasmoid sounding using the GSFC raytracer are described in [21].
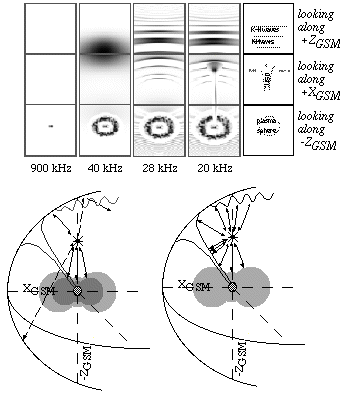
In Figure 4 the simulated returns for frequencies corresponding to several densities using the high frequency simulation are shown. The figures have been inverted to make viewing easier, so that dark areas indicate strong signal returns. Each panel is comprised of 3 sub-panels, each of which shows a 90 degree field of view along a GSM axis (+ZGSM, +XGSM, and -ZGSM from top to bottom). The subpanels have been combined to form mosaics which show strips running from below the spacecraft to above it along the nose of the magnetosphere. The spacecraft was assumed to be at <0,0,8 RE>GSM (i.e. above the north pole) for these simulations. The panels were all generated at the 1 ° x1 ° resolution estimated by Calvert . The first panel shows returns from 900 kHz waves which penetrate everything but the polar ionosphere. At this frequency, the sounder is acting as a topside sounder, since the transmitted frequency exceeds the plasma frequency of all other magnetospheric structures. The second panel shows echoes from a 40 kHz sounding, where the returns highlight more of the geometry of the plasmasphere as well as two reflections off the boundary layers to the north and south. The third panel uses a 28 kHz transmission to reveal Kelvin-Helmholtz waves on the inner boundary layers, as well as the plasmasphere. Comparing the second and third panels illustrates a sounder's ability to distinguish between different boundary layer configurations, which can be difficult to differentiate via in-situ measurements (Fig. 5) [22]. The final panel is at 20 kHz, which is high enough to pass through the tail lobes and the auroral cavity, but low enough to be reflected by most magnetospheric structures. Although most of the cusp returns are very weak, one segment and one spot have gradients which return waves to the sounder. The locations of the returns depend on the location of the sounder as well as the geometry of the cusp and magnetopause/boundary layers. At certain sounding frequencies, the cusp shows clearly by virtue of its blocking of portions of the boundary layer echoes from the dayside magnetopause. The rapid sampling of the cusp position and velocity by the sounder would significantly aid in understanding the response of the high altitude cusp to changing IMF conditions. The sounder design discussed by Calvert would sound to both higher and lower densities than are shown here.
For comparison, a sequence of skymaps showing the motion of a surface wave in the boundary layers is shown using the GSFC raytracer in Fig. 5. These images are analogous to the +ZGSM facing segments of Figs. 2 and 3 at several subsequent times. This simulation also conforms to the sounder described by Calvert, but does not have as many sub-models as the high frequency simulation. In this figure the gray scale does not correspond to a true intensity (as in Figs. 2, 3), but rather to a 'ray missed distance', which is an analog for echo power flux.
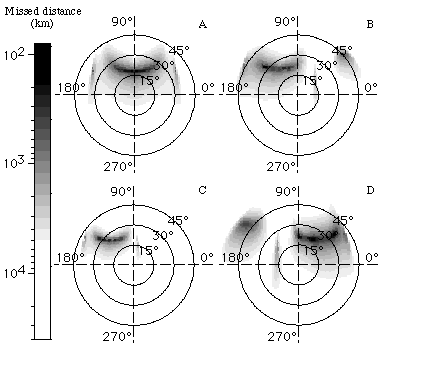
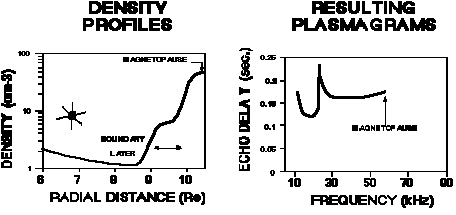
These simulated radio images are only one way of organizing the echo data. From the returns and their time delays, it is possible to determine the density and field strength at each point that reflects a wave to the sounder. At the same time, from Doppler and other information, velocity profiles can also be constructed from the same returns. Simulated plasmagrams, and the density profiles that were used by the Goddard plasma wave raytracer to generate them, are shown in Fig. 6. Plasmagrams are another selectable output of the simulation software which directly simulate the process by which an actual sounder would probe the magnetosphere.
[2] B. W. Reinisch, Radio Science, 21, 331 (1986).
[3] J. E. Jackson, AlouetteISIS Program Summary, NSSDC/WDCAR&S 86, NASA Goddard Space Flight Center, Greenbelt MD (1986).
[4] P. L. Dyson and J. D. Winningham, J. Geophys. Res., 79, 521 (1974).
[5] W. Calvert, R. F. Benson, D. L. Carpenter, S. F. Fung, D. L. Gallagher, J. L. Green, D. M. Haines, P. H. Reiff, B. W. Reinisch, M. F. Smith, and W. W. L. Taylor, in press, Radio Science (1995).
[6] F. F. Chen, Introduction to Plasma Physics, Plenum Press, New York (1974).
[7] T. H. Stix, Waves in Plasmas, American Institute of Physics, New York (1992).
[8] J. L. Green, and D. A. Gurnett, Geophys. Res. Lett., 7, 65 (1980).
[9] Y. Omura, and J. L. Green, J. Geophys. Res., 98, 9189 (1993).
[10] S. Fung, J. L. Green, W. W. L. Taylor, M. F. Smith, R. F. Benson, W. Calvert, D. L. Carpenter, D. L. Gallagher, P. H. Reiff, and B. W. Reinisch, submitted to Geophys. Res. Lett. (1995).
[11] P. H. Reiff, Magnetopause Mapper (Ionosonde), Section 6.5, Space Physics Missions Handbook, R. A. Cooper and D. H. Burks eds., NASA OSSA (1991).
[12] J. L. Green and S. F. Fung, Adv. Space Res., 14, 217(1994).
[13] B. W. Reinisch, private communication, 1995.
[14] D. A. Gurnett and R. R. Anderson, in Physics of Auroral Arc Formation, Geophys. Monogr. Ser., 25, Akasofu and Kan, eds. (American Geophysi cal Union, Washington, D.C., 1981), p. 341.
[15] R. F. Benson, M. M.. Mellott, R. L. Huff, and D. A. Gurnett, J. Geophys. Res., 93, 7515 (1988).
[16] W. S. Kurth, D. A. Gurnett, R. R. Anderson, J. Geophys. Res., 86, 5519 (1981).
[17] D. Morgan and D. A. Gurnett, J. Geophys. Res., 96, 9595 (1991).
[18] D. P. Stern, J. Geophys. Res. 86, 5839 (1981).
[19] D. G. Sibeck, R. A. Lopez, and E. C. Roelof, J. Geophys. Res., 96, 5489 (1981).
[20] J. L. Green, Raytracing of planetary radio emissions, Planetary Radio Emissions II, Proceedings of the 2nd international workshop held at Graz, (Austrian Academy of Science, Vienna, 1988), p. 355.
[21] P. H. Reiff, J. L. Green, R. F. Benson, D. L. Carpenter, W. Calvert, S. F. Fung, D. L. Gallagher, Y. Omura, B. W. Reinisch, M. F. Smith, and W. W. L. Taylor, Remotes sensing of substorm dynamics via radio sounding, Substorms 2, Proceedings of the Second Intl. Conference on Substorms, J. R. Kan, J. D. Craven, and S. I. Akasofu, eds. (U of Alaska Press, Fairbanks, 1994), p. 261.
[22] N. Sckopke, G. Paschmann, G. Haerendel, B. U. Sonnerup, S. J. Bame, T. G. Forbes, E. W. Hones, and C. T. Russell, J. Geophys. Res., 86, 2099 (1981).
[23] Since this talk was given, ring current models have been added to the GSFC simulation.
[24] The authors may also be reached via electronic mail at: