Remote Sensing of Substorm Dynamics via Radio Sounding

P. H. Reiff, J. L. Green, R. F. Benson, D. L. Carpenter, W. Calvert, S. F. Fung, D. L. Gallagher, Y. Omura, B. W. Reinisch, M. F. Smith and W. W. L. Taylor

Proceedings of the Second International Conference on Substorms, Ed. J. R. Kan, J. D. Craven and S.-I. Akasofu, University of Alaska Press, Fairbanks, Alaska, 281-287, 1994.

Reprinted with Permission from Geophysical Institute, Copyright 1995

Abstract

This paper describes the technique of magnetospheric radio sounding and shows how it can be applied to produce "images" of magnetospheric electron density distributions and their variations during substorms. The magnetospheric radio sounder is based on more than a half-century heritage of ionospheric sounding combined with modern digital techniques. Coded pulses are transmitted by a long dipole and the delay times and directions-of-arrival of the returning pulses are measured. Plasma densities from 0.1 to 10⁵ cm^-3 can be remotely sensed simultaneously along several different directions by a digital sounder operating in the 3 kHz to 3 MHz range. Positions of magnetospheric plasma and magnetic boundaries, such as the plasmapause and magnetopause, can be monitored on a time scale of a few minutes, and plasmaspheric erosion and refilling quantified during a substorm cycle. Such measurements have previously been impossible to obtain. From a sounder suitably situated in the near-earth tail lobe, one can measure the magnetotail cross-section and get information on the field strength, thus allowing monitoring of total tail flux changes during a substorm and thus the difference between dayside and nightside merging rates. It may also be possible to sound a near-Earth plasmoid directly and thus sense its position, growth, and motion.

INTRODUCTION

The Earth's magnetosphere is extremely dynamic, with large-scale changes in size and shape in response to interplanetary conditions, and major internal reconfigurations in response to substorms. Single-spacecraft measurements allow determination of magnetospheric conditions only at specific points at any given time. Remote sensing techniques, such as auroral imaging, can aid our understanding tremendously by allowing monitoring of the footprint of some of the plasma domains. Auroral images, however, reflect only precipitating particles; particles trapped in the equatorial plane or those in the magnetospheric boundary layers typically do not precipitate at all. Remote sensing by means of far ultraviolet (FUV), extreme ultraviolet (EUV), X-ray, and energetic neutral atom (ENA) detection promises a great step forward in monitoring magnetospheric domains [Williams et al., 1992].

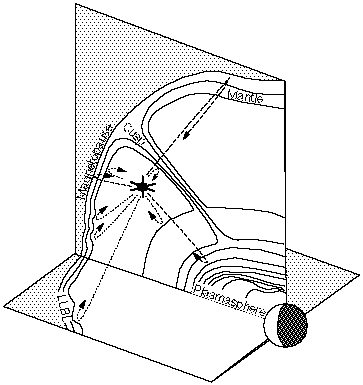
During the NASA Space Physics Strategy-Implementation Study of 1990, we suggested using radio sounders to study the magnetopause and its boundary layers [Reiff, 1991], and to study the plasmasphere [Green and Fung, 1994]. The magnetopause, plasmasphere, as well as the cusp and boundary layers, can be remotely monitored if a radio sounder is placed on a high-inclination polar-orbiting spacecraft with a reasonable (>=6 RE) apogee (Figure 1, from Reiff et al. [1994]).

Figure 1. Schematic contours of constant plasma density in the sunward side of the magnetosphere. A radio sounder on a polar-orbiting spacecraft can remotely sense the density structures at the magnetopause, the plasmapause, the auroral density cavity and the magnetospheric cusp, thus creating quantitative "images". Lower-frequency waves (dotted) probe the low-density surfaces, while higher-frequency waves (dashed) probe the higher-density structures. Waves on the boundaries yield multiple reflecting points, allowing a crude image within a few minutes and a composite image as illustrated within the time required for a quarter of a spacecraft orbit, by combining successive electron density profiles along the orbit [from Reiff et al., 1994].

Radio sounding techniques date back to the study of the ionosphere by Breit and Tuve [1926]. Swept-frequency ground-based sounders are used to monitor the electron number density (Ne) structure of the ionosphere up to the F-layer density peak with high time resolution. The early instruments evolved into a global network which produced high-resolution ionograms (displays of echo delay versus frequency) on 35 mm film. The bottomside electron density profiles deduced from these records provided one of the cornerstones of the success of the International Geophysical Year [Berkner, 1959].

Topside ionospheric densities, above the F-layer density maximum, were first measured in the Alouette/ISIS (International Satellites for Ionospheric Studies) program [Franklin and Maclean, 1969; Jackson et al., 1980]. A series of consecutive profiles can be combined to create orbital-plane Ne contours from the satellite altitude to the altitude of the F layer peak density [Nelms and Lockwood, 1966 and Benson, 1985 and references therein]. Comparisons of densities from topside and bottomside sounders, and multi-spacecraft studies have indicated that the error of the Alouette/ISIS-derived Ne values is typically within 10%, even at the most remote distances [Whitteker et al., 1976; Hoegy and Benson, 1988 and references therein]. ISIS demonstrated the synergism between sounders and optical imagers on the same spacecraft [Lui and Anger, 1973; Shepherd et al., 1976]. Digital technology was used in later spacecraft sounders, such as in Japan's ISS-b (Ionosphere Sounding Satellite), Ohzora (also called EXOS-C), and Akebono (or EXOS-D) spacecraft; and in the USSR's Intercosmos 19 and Cosmos 1809 missions [see Green et al. 1994 and references therein]. ISIS also showed the ability to remotely sound the magnetospheric cusp [Dyson and Winningham, 1974]. The ISIS-C spacecraft would have contained a sounder with a similar orbit and similar science objectives to that discussed here, but was never flown [J. D. Winningham, personal communication, 1994].

Bottomside (ground-based) ionospheric sounders have enjoyed great advances over the last few decades [Hunsucker, 1991]. These advanced ionospheric sounders can measure the frequency, time delay, amplitude, phase, Doppler shift and spread, polarization, and direction of arrival of the echo. Two sounders in this class are the Dynasonde (developed at the U.S. Department of Commerce Laboratories in Boulder) and the Digisonde (developed at the University of Massachusetts Lowell). These instruments offer a high degree of flexibility in measurement format since their operations are controlled by software [Reinisch, 1986]. Evidence that their scientific capabilities go far beyond the Ne profiles of the standard ionosondes is indicated from results that show, for example, turbulence, drifts, winds and structures [Wright and Hunsucker, 1983; Buchau et al., 1988]. A new generation of spaceborne sounders can use these latest techniques [Reinisch et al., 1992] to make sounding of the magnetosphere possible with very modest power requirements by taking advantage of spread spectrum pulse compression and Fourier transform processing. A 500m tip-to-tip dipole is planned as transmitting antenna.

RADIO WAVE SOUNDING OF THE MAGNETOSPHERE

Radio wave sounding of the magnetosphere uses the same fundamental principles as ionospheric sounding. A cold magnetized plasma supports two freely propagating electromagnetic waves, the O (ordinary) and X (extraordinary) modes, each with distinct phase velocity and polarization [e.g., Chen, 1974]. The propagation characteristics of these waves are determined by the local electron plasma frequency, fp , and electron gyrofrequency, fg.

Figure 2 shows the variation of the square of the ratio of the wave phase velocity vph to the speed of light c on a scale of increasing frequency, for several wave modes. The cross-hatched regions represent the forbidden frequency ranges in which the indicated waves cannot propagate. The Z mode has a lower frequency cutoff fz (when vph²/c² = [[infinity]]) and an upper frequency resonance (when vph²/c² = 0) that restricts its propagation and is thus referred to as a trapped mode of the plasma. This wave mode is unsuitable for use in direct sounding to great distances. The whistler mode (not shown in the figure) is also a trapped mode.

Figure 2. A schematic phase velocity -frequency diagram showing the ordinary (O Mode) and extraordinary (X Mode) propagation modes supported by a cold plasma. (The shaded areas indicate regions of non-propagation). The extraordinary mode has two branches. The lower frequency branch (often called the Z mode) is trapped between a lower frequency cutoff fz and an upper resonant frequency varying between fp and fuh, depending on the angle of propagation [Ratcliffe, 1959]. The high frequency branch is normally referred to as the X mode. For the purposes of remote sensing, the O and X modes are used because they propagate at all frequencies above their cutoffs at fp and fx, respectively. From a knowledge of the plasma frequency, the electron density can be derived; from the fx frequency, the gyrofrequency (and thus the field strength) can be derived. [Adapted from Chen, 1974.]

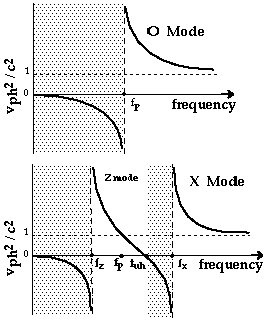
Since the X and O modes have no propagation restrictions above their low frequency cutoffs (Figure 2), they are suitable for remote radio sounding. The cutoff for the O mode is the local plasma frequency fp,

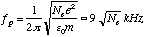(1)

when Ne is expressed in cm^-3; [[epsilon]]o is the permittivity of free space, e is the electron charge and m is the electron mass. For the X mode, the cutoff fx is

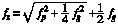(2)

where

fg = (1/2[[pi]])eB/m = 28.0 B (Hz) (3)

when B, the magnetic field strength, is expressed in nT. These two modes propagate freely with group velocity vg ~ vph ~ c when the wave frequencies are well beyond the plasma cutoffs; thus they are called the free-space modes.

A swept-frequency sounder transmits and receives a sequence of X and O mode pulses, with the frequencies increasing stepwise. When the transmitted waves enter a region of increasing plasma density or magnetic field strength, the pulse is reflected when the wave frequency matches the cutoff frequency. Most of the inner magnetosphere has a relatively low density - thus a satellite lies between increasing density gradients at the magnetopause and at the plasmasphere (see Figure 1). For most magnetospheric applications the primary echo paths will be approximately perpendicular to the plasma density contours at reflection. A data record (plasmagram) consists of the time delay and amplitude, along with complex Doppler and angle-of-arrival information, for each sounding frequency and polarization.

Thus the swept-frequency measurements permit the determination of the electron plasma density profiles of remote plasma regions [see, e.g., Jackson et al., 1980; Huang and Reinisch, 1982], so long as the density is generally increasing with distance. Magnetospheric density structures are quite dynamic in space and in time. Thus each transmission will typically result in more than one echo (Figure 3). Returns will usually be obtained from several directions for the same frequency transmission, but each will exhibit a different time delay, angle of return, and Doppler shift, thereby allowing a rough cross-section within minutes. From a sequence of profiles taken during a portion of a single orbit, one can produce two-dimensional, cross-sectional magnetospheric images (Figure 1). Raytracing studies indicate that from a dayside position much as in Figure 1, signal returns would also be received from the dawn and dusk magnetopause [Fung et al., 1994]. Thus information on the 3-D magnetospheric Ne structures will also be obtained. For more information on the technique and applications of magnetospheric radio sounding, see Green et al. [1993], Reiff et al. [1994], Fung et al.[1994], Green et al.[1994], and Calvert et al. [1994].

THE USE OF SOUNDING IN SUBSTORM STUDIES

A radio sounder is ideal for studying the global structure and dynamics of the plasmasphere and its outer boundary, the plasmapause. The plasmasphere reacts sensitively to changes in magnetospheric convection, with the plasmapause varying in geocentric distance between 2 and 7 RE as magnetospheric conditions change from active to quiet [Carpenter, 1966; Spiro et al., 1981]. A radio sounder is ideally suited to study such dynamic changes since it can provide a sequence of nearly instantaneous plasmaspheric electron density profiles. Therefore, nearly the same region can be probed repeatedly within minutes, allowing us to separate spatial from temporal variations. Thus a sounder can provide, for the first time, observations of the formation of a plasmapause boundary at a new location during substorms, and of plasmatrough refilling beyond a newly formed plasmapause. Under certain viewing conditions, the distribution and movements of dense plasmas being eroded from the main plasmasphere during substorms can be observed, thus permitting the study of the development of outlying "detached" or "connected" cold plasma regions. The possible decoupling of the high altitude and low altitude convection regimes can also be investigated [e.g. Carpenter et al., 1993]

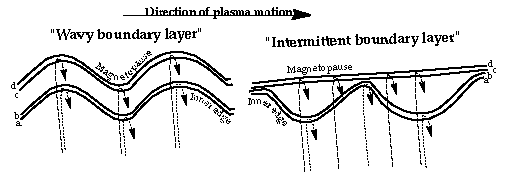
A sounder, by monitoring the location of the magnetopause and the time evolution of the magnetopause boundary layers, can determine (1) the variability of plasma mantle density and thickness in response to the southward and westward components of the IMF, and (2) the passage of wave structures in the low-latitude boundary layer [Rosenbauer et al., 1975; Paschmann et al., 1978; Paschmann, 1984]. One can readily determine from a sequence of sounder measurements whether the inner edge of the boundary layer moves only in phase with the magnetopause motion (Figure 3, left), or whether the thickness of the layer varies in time as the plasmas move downstream (Figure 3, right [from Reiff et al., 1994]).

Figure 3. A sequence of reflections from density gradients at the magnetopause and the inner edge of the boundary layer (contours are labeled a, b, c and d in increasing density). From ISEE 1 and 2, we know that the boundary layer has a relatively sharp density gradient at the magnetopause and a sharp gradient at the inner edge, with a "ledge" in between [Sckopke et al., 1981; Song et al., 1990], and that these boundaries are constantly in motion. It is not known, however, if the thickness of the boundary layer is nearly constant (left) or variable (right). From successive soundings at low (dotted) and high (dashed) frequencies as the structures pass by the spacecraft, this question should be resolved [from Reiff et al., 1994].

A radio sounder, by using its direction-finding capability [Calvert et al., 1994], can determine the distance from the spacecraft to one or more locations on the magnetopause simultaneously [Fung et al., 1994]. By comparing sounder observations with simultaneous solar wind data from solar wind monitoring spacecraft such as WIND and IMP-8, one can test the solar wind dependence of empirical magnetopause models such as Sibeck et al. [1991], Roelof and Sibeck [1993], and Petrinec and Russell [1993a, b].

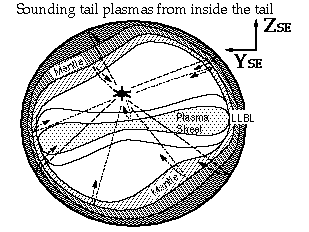
In the special case of spacecraft near apogee in the near-Earth magnetotail (or a lunar-based instrument when the Moon is in the magnetotail [Reiff, 1991; Green and Fung, 1994]), one can receive the reflected signals from both the dawn and duskside equatorial magnetopause and north and south high latitude magnetopause nearly simultaneously (Figure 4). It can then determine whether the magnetospheric tail is flattened and/or twisted by the IMF, as has been proposed [e.g. Fairfield, 1992 and references therein]. By determining the size of the magnetotail and having some information about the field strength derived from the X mode echoes, it will be possible to monitor the magnetic flux in the magnetotail and thus the net (dayside minus tail) magnetic merging rates [Russell and McPherron, 1973]. Note that a sounder system located in the high-latitude lobes may be able to sound through the low-density plasmasheet to the far side magnetopause.

Figure 4. A schematic of reflections from density gradients at the magnetopause and its boundary layers from a spacecraft (or a lunar base) within the cislunar magnetotail lobe. The concave density cavity provides an enhancement of the return signal and allows multiple returns from a single transmission, yielding a multipoint tail cross-section on less than minute time scales. The plasma sheet is of such low density that middle- (dash-dot) and high-frequency signals (dashed) can sound right through to reach the far boundary layer and magnetopause, or a low-frequency signal (dotted) can probe the near edge of the plasmasheet from the lobe. (Beyond lunar distance, most of the lobe is full of plasma and the density contrast at the plasma sheet is insufficient for a signal return, but the magnetopause should still yield a detectable signal).

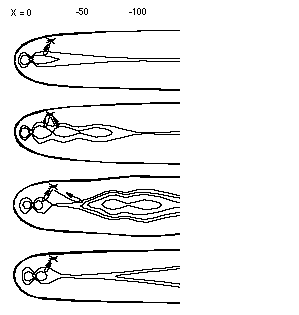
In certain geometries, it may also be possible to monitor the growth and motion of plasmoids in the magnetotail. In the near-earth neutral line model of a substorm [Hones, 1979], a plasmoid forms, grows, and disconnects in a substorm cycle [e.g. Baker et al., 1987; Slavin et al., 1989]. If a sounder is situated in the high-latitude lobes (e.g., at XSM ~-20 RE, |ZSM| ~10), it may be able to sound off the density enhancement of the growing and moving plasmoid. A schematic of this reflection geometry is shown in Figure 5 (adapted from Richardson and Cowley, 1987]. In the near-earth magnetotail (<100 RE), the magnetotail lobe density is much smaller than the plasmasheet density [Slavin et al., 1985] and a sounder should be able to remotely sense a plasmoid. In the distant (>100 RE) magnetotail, however, the lobes have a great deal of plasma in them and the density contrast is not sufficient to return an echo from the plasmoid [Frank and Paterson, this volume].

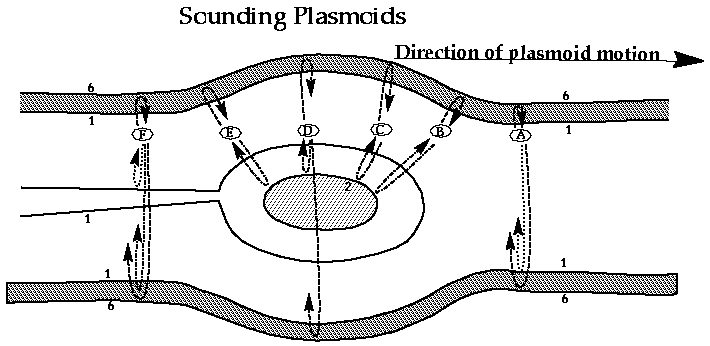
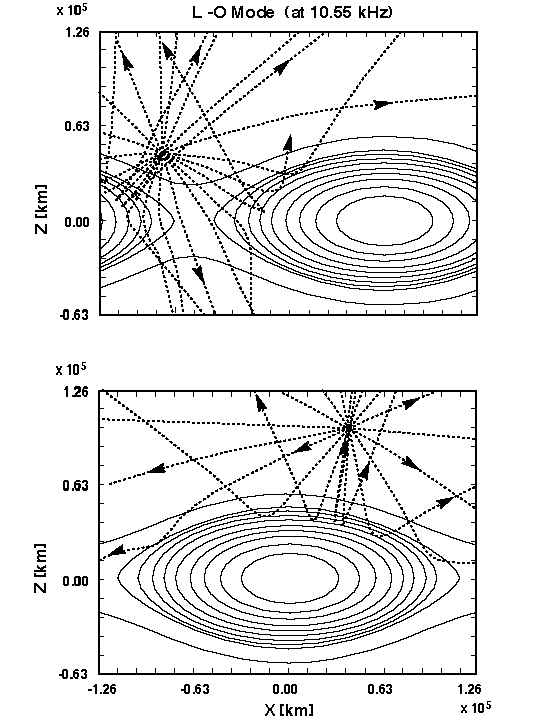
Figure 5. A schematic of reflections of sounder rays (dashed) from density gradients associated with plasmoids. A sounder situated in the low-density magnetotail lobe may be able to monitor the growth and motion of a plasmoid during the substorm cycle [adapted from Richardson and Cowley, 1987].

A plasmoid moving down tail past the sounder may allow a sequence of soundings to yield information on the growth and motion of the plasmoid, and monitoring of the deformation of the magnetopause as the plasmoid moves [e.g. Slavin et al., 1993]. A schematic of the possible geometry is shown in Figure 6. As a first test of this idea, we have taken the MHD plasmoid model developed by Omura and Green [1993] and performed raytracing calculations with a test sounder in the near-Earth magnetotail lobe. A set of sample rays emanating from the spacecraft are shown bouncing off of the plasmoid (Figure 7). Here the sounding frequency is near 11 kHz, corresponding to a density of about 1.5 cm^-3. Divergence of the rays as they refract off the plasmoid indicate the defocusing aspect of the convex surface [Reiff et al., 1994; Calvert et al., 1994].

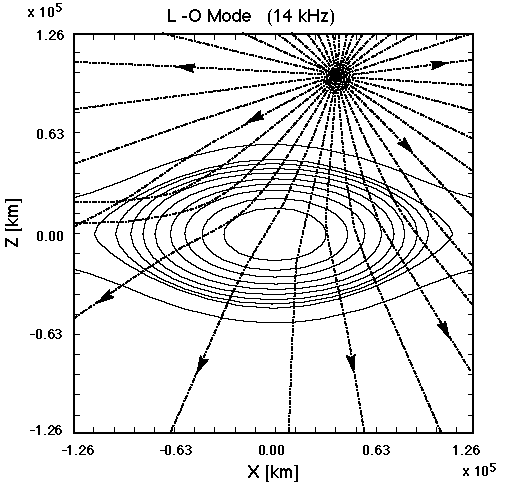
Higher sounding frequencies can penetrate the plasmoid and may allow sounding of the far side magnetopause. Figure 8 shows a raytracing at 14 kHz (corresponding to 2.4 cm^-3density), the minimum frequency which will traverse the plasmoid. Higher frequency pulses will exhibit less refraction than shown here. The return signal from the far magnetopause will be weak, since the reflecting surface is far away; however, the signal should be focused from the concave nature of the magnetopause and may well be detectable.

Figure 6. Schematic of sounding off a plasmoid from a cislunar magnetotail location as the plasmoid moves downtail. A sounder will effectively move from locations A, to B, C, etc. The highest frequency transmissions (shown dashed) pass through the plasmoid and/or the plasma sheet and reflect from the magnetopause; middle frequencies (dash-dot) sense the plasmoid or the boundary layer, whichever is closer along that line of sight. The lowest frequencies (dotted) sense the plasma sheet or lowest-density boundary layer, whichever is nearer.

Figure 7. Raytracing of sounder rays at 10.5 kHz (dashed) from density gradients associated with a plasmoid. The plasmoid density contours and raytracing techniques are described in Omura and Green [1993]. The top panel indicates the reflections observed if the sounder is situated above an x-line; the bottom panel indicates the reflections observed if a plasmoid passes under the sounder. (The plasma frequency in the lobe is 9.5 kHz in this simulation; the peak in the plasmoid is 12.2 kHz).

CONCLUSIONS

A magnetospheric radio sounder can provide quantitative electron density profiles simultaneously in several different directions. From a sequence of these profiles, contour plots of the density structure in the orbital plane can be constructed, with some out-of-plane information as well. This capability will allow the remote sensing of magnetospheric topology and plasma domains on minute time scales. The application of the sounder technique to substorm studies is straightforward and powerful. If the density contrast between the plasmoid and the background lobe plasma is sufficient (and it should be in cislunar space), a sounder in an appropriate location should be able to monitor plasmoid formation, growth and motion and thus remotely sense major substorm reconfigurations in the magnetotail.

Figure 8. Similar to figure 7, but for a sounder frequency of 14 kHz (corresponding to 2.4 cm^-3), just above the plasma frequency in the center of the plasmoid (12.2 kHz). This frequency (and all higher frequencies) will penetrate the plasmoid and can be used to sense the distant magnetopause. Higher frequency rays will be refracted less than shown here.

Acknowledgements We would like to acknowledge early discussions of this idea with Stan Shawhan, who gave us (PHR and JLG) strong encouragement. We acknowledge helpful discussions with David Winningham and Roger Anderson. The work at Rice University was supported by NASA under grant NAGW 1655, and at Nichols Research Corporation under contract 507854-f.

REFERENCES

Baker, D. N., R. C. Anderson, R. D. Zwickl, and J. A. Slavin, Average plasma and magnetic field variations in the distant magnetotail associated with near-Earth substorm effects, J. Geophys. Res., 92, 71-81, 1987.

Benson, R. F., Auroral kilometric radiation: Wave modes, harmonics, and source region electron densities, J. Geophys. Res., 90, 2753-2784, 1985.

Berkner, L. V., The international geophysical year, Proc. IRE, 47, 133-136, 1959.

Breit, G., and M. A. Tuve, A test for the existence of the conducting layer, Phys. Rev., 28, 554-575, 1926.

Buchau, J., B. W. Reinisch, D. N. Anderson, E. J. Weber, and C. Dozois, Polar cap plasma convection measurements and their relevance to the modeling of the high-latitude ionosphere, Radio Sci., 23, 521-536, 1988.

Calvert, W., R. F. Benson, D. L. Carpenter, S. F. Fung, D. Gallagher, J. L. Green, P. H. Reiff, B. W. Reinisch, M. F. Smith, and W. W. L. Taylor, The feasibility of radio sounding of the magnetosphere, to be submitted to J. Geophys. Res., 1994.

Carpenter, D. L., B. L. Giles, C. R. Chappell, P. M. E. Decreau, R. R. Anderson, A. M. Persoon, A. J. Smith, Y. Corcuff, and P. Canu, Plasmasphere dynamics in the duskside bulge region: a new look at an old topic, J. Geophys. Res., 98, 19,243-19,271, 1993.

Carpenter, D. L., Whistler evidence of a "knee" in the magnetospheric ionization density profile, J. Geophys. Res., 71, 693, 1966.

Chen, F. F., Introduction to Plasma Physics, Plenus Press, N.Y., 1974.

Dyson, P. L. and J. D. Winningham, Top side ionospheric spread F and particle precipitation in the day side magnetospheric clefts, J. Geophys. Res., 79, 5219, 1974.

Fairfield, D. H., On the structure of the distant magnetotail: ISEE-3, J. Geophys. Res., 97, 1403-1410, 1992.

Franklin, C. A., and M. A. Maclean, The design of swept-frequency topside sounders, Proc. IEEE, 57, 897-929, 1969.

Fung, S. F., R. F. Benson, J. L. Green, M. F. Smith, D. L. Carpenter , W. Calvert, D. L. Gallagher, P. H. Reiff, B. W. Reinisch, and W. W. L. Taylor, Probing the Magnetopause and Boundary Layers by the Radio Sounding Technique, J. Geophys. Res., submitted, 1994.

Green, J. L., and S. F. Fung, Radio sounding of the magnetosphere from a lunar-based VLF array, Adv. Space Res., 14, 217-221, 1994.

Green, J. L., R. F. Benson, W. Calvert, S. F. Fung, P. H. Reiff, B. W. Reinisch, and W. W. L. Taylor, A Study of Radio Plasma Imaging for the proposed IMI mission, NSSDC Technical Publication, Goddard Space Flight Center, February, 1993.

Green, J. L., R. F. Benson, D. L. Carpenter, W. Calvert, S. F. Fung, D. Gallagher, P. H. Reiff, B. W. Reinisch, M. Smith, and W. W. L.. Taylor, Radio sounding of the magnetosphere, to be submitted to J. Geophys. Res., 1994.

Hoegy, W. R., and R. F. Benson, DE/ISIS conjunction comparisons of high-latitude electron density features, J. Geophys. Res., 93, 5947-5954, 1988.

Hones, E. W., Jr., Transient phenomena in the magnetotail and their relationship to substorms, Space Sci. Rev., 23, 393, 1979.

Huang, X., and B. W. Reinisch, Automatic calculation of electron density profiles from digital ionograms. 2. True height inversion of topside ionograms with the profile-fitting method, Radio Science, 17, 837-844, 1982.

Hunsucker, R. D., Radio Techniques for Probing the Terrestrial Ionosphere, Vol. 22, Phys. Chem. Space, Springer Verlage, Berlin, 1991.

Jackson, J. E., E. R. Schmerling, and J. H. Whitteker, Mini-review on topside sounding, IEEE Trans. Antennas Propagat., AP-28, 284-288, 1980.

Lui, A. T. Y., and C. D. Anger, Uniform belt of diffuse auroral emissions seen by the ISIS 2 scanning photometer, Planet. Space Sci., 21, 799-809, 1973.

Nelms, G. L., and G. E. K. Lockwood, Early results from the topside sounder in the Alouette II satellite, in Space Research VII, edited by R. L. Smith-Rose, EB pp. 604-623, North-Holland Publishing Co., Amsterdam, 1966.

Omura, Y. and J. L. Green, Plasma wave signatures in the magnetotail reconnection region: MHD simulation and ray tracing, J. Geophys. Res., 98, 9189-9199, 1993.

Paschmann, G., N. Sckopke, G. Haerendel, I. Papamastorakis, S. J. Bame, J. R. Asbridge, J. T. Gosling, E. W. Hones Jr. and E. R. Tech, ISEE plasma observations near the subsolar magnetopause, Space Sci. Rev., 22, 717-737, 1978.

Paschmann, G., Plasma and particle observations at the magnetopause: implications for reconnection, in Magnetic Reconnection in Space and Laboratory Plasmas, Geophys. Monogr. Ser., 30, edited by E. W. Hones Jr., pp. 114-123, AGU Press, Washington, D.C., 1984.

Petrinec, S. M., and C. T. Russell, External and internal influences on the size of the dayside terrestrial magnetosphere, Geophys. Res. Lett., 20, 339, 1993a.

Petrinec, S. M., and C. T. Russell, An empirical model of the size and shape of the near-earth magnetotail, Geophys. Res. Lett., 20, 2695, 1993b.

Ratcliffe, J. A., The magneto-ionic theory and its application to the ionosphere, 206 pp., Cambridge University Press, New York, 1959.

Reiff, P. H., Magnetopause Mapper (Ionosonde), Section 6.5, Space Physics Missions Handbook, ed. R. A. Cooper and D. H. Burks, NASA OSSA, 1991.

Reiff, P. H., J. L. Green, R. F. Benson, D. L. Carpenter, W. Calvert, S. F. Fung, D. L. Gallagher, B. W. Reinisch, M. F. Smith and W. W. L. Taylor, Radio imaging of the magnetosphere, EOS, Trans. AGU, 75, 129-134, 1994.

Reinisch, B. W., New techniques in ground-based ionospheric sounding and studies, Radio Science, 21, 3, pp. 331-341,1986.

Reinisch, B. W., D. M. Haines, and W. S. Kuklinski, The new portable Digisonde for vertical and oblique sounding, AGARD Proceedings Number 502, pp. 11-1 to 11-11, 1992.

Richardson, I. G. and S. W. H. Cowley, Plasmoid-associated energetic ion bursts in the distant geomagnetic tail, in Magnetotail Physics, edited by A. T. Y. Lui, pp. 251-256, The Johns Hopkins University Press, Baltimore, 1987.

Roelof, E. C. and D. G. Sibeck, The magnetopause shape as a bivariate function of IMF Bz and solar wind dynamic pressure, J. Geophys. Res., 98, 21,421-21,450, 1993.

Rosenbauer, H., H. Grunwaldt, M. D. Montgomery, G. Paschmann and N. Sckopke, Heos 2 plasma observations in the distant polar magnetosphere: The plasma mantle, J. Geophys. Res., 80, 2723-2737, 1975.

Russell, C. T. and R. L. McPherron, The magnetotail and substorms, Space Sci. Rev., 15, 205, 1973.

Sckopke, N., G. Paschmann, G. Haerendel, B. U. Ö. Sonnerup, S. J. Bame, T. G. Forbes, E. W. Hones, Jr., and C. T. Russell, Structure of the low-latitude boundary layer, J. Geophys. Res., 86, 2099-2110, 1981.

Shepherd, G. G., J. H. Whitteker, J. D. Winningham, J. H. Hoffman, E. J. Maier, L. H. Brace, J. R. Burrows, and L. L. Cogger, The topside magnetospheric cleft ionosphere observed from the ISIS 2 spacecraft, J. Geophys. Res., 81, 6092-6102, 1976.

Sibeck, D. G., R. A. Lopez, and E. C. Roelof, Solar wind control of the magnetopause shape, location, and motion, J. Geophys. Res., 96, 5489-5496, 1991.

Slavin, J. A., et al., CDAW 8 observations of plasmoid signatures in the geomagnetic tail: An assessment, J. Geophys. Res., 94, 15,153-15,175, 1989.

Slavin, J. A., M. F. Smith, E. L. Mazur, D. N. Baker, E. W. Hones, Jr., T. Iyemori, and E. W. Greenstadt, ISEE 3 observations of traveling compression regions in the Earth's magnetotail, J. Geophys. Res., 98, 15,425-15446, 1993.

Song, P., R. C. Elphic, C. T. Russell, J. T. Gosling, and C. A. Cattell, Structure and properties of the subsolar magnetopause for northward IMF: ISEE observations, J. Geophys. Res., 95, 6375-6387, 1990.

Spiro, R. W., M. Harel, R. A. Wolf, and P. H. Reiff, Quantitative simulation of a magnetospheric substorm, 3. Plasmaspheric electric fields and evolution of the plasmapause, J. Geophys. Res., 86, 2261-2272, 1981.

Whitteker, J. H., L. H. Brace, E. J. Maier, J. R. Burrows, W. H. Dodson, and J. D. Winningham, A snapshot of the polar ionosphere, Planet. Space Sci., 24, 25-32, 1976.

Williams, D., E. C. Roelof, and D. G. Mitchell, Global magnetospheric imaging, Rev. Geophys., 30, 183-208, 1992.

Wright, J. W., and R. D. Hunsucker, Estimation of turbulent energy dissipation, winds, and ionospheric structures from Dynasonde measurements, Radio Sci., 18, 988-994, 1983.

Return to scientific documents page

Return to the IMAGE Home Page

Dr. D. R. Williams, dwilliam@nssdc.gsfc.nasa.gov, (301) 286-1258
NSSDC, Mail Code 633, NASA/Goddard Space Flight Center, Greenbelt, MD 20771